Cultural research into magic squares

This page consists of research notes in progress, concerning magic squares. If you have information to share, or can clarify anything here, please contact me.

Also see:
Research index page
Magic squares in cultural history

Temporary key:

External link: EXL
Internal link within current section: INL
Internal link to another section: INL (secname)

Introduction: about magic squares

check for duplication and concatenate with: this page.

Magic squares are matrices of n x n numbers in which each column, row and diagonal all sum to a common number [INL: formulas]. Magic cubes (and hyper-cubes [INL: hyper-cubes]) are the same in 3 (or more) dimensions.

[IMG: a square and a cube with numbers but no lines]

Setting aside rotations and reflections (regarded as trivial variations) there is only one order 3 square, 880 order 4 squares, and 275,305,224 order 5. The number of variations for orders 6 and 7 has, to date, only been estimated (Pinn and Wieczerkowski).

To give an idea of the sheer numbers of variations from order 5 upwards, drawing 75 magic squares by hand every day for nearly 10 years would cover all the order 5 variations.

Within and throughout the sets are further subsets that obey particular rules [subset examples e.g. latin squares, (others from Pickover_reviewed_notes.rtf) perfect squares, knight's move (which can produce imperfect) and other patterns, etc.].

Each set of magic squares of a particular order (e.g. all the order 4 squares) exists within various supersets determined by certain shared properties. The simplest distinction made between magic matrices is between those formed by odd, even and 'odd-even' (or 'oddly-even') numbers. The term oddly-even describes even numbers (6, 10, 14, 18...) that yeild an odd number when divided by 2. The reason for these distinctions is that magic matrices of these 3 types differ from each other in significant ways, and share certain unique properties between themselves.

[IMG: magic lines and numbers from squares - 1 each of the 3 types]

Magic squares have been used in image watermarking (Huang 2009) and encryption algorithms (Ganapathy and Mani 2009). Anyone discovering squares of [TYPE?] are requested to offer it for military use [EXL source].

References: introduction

Ganapathy, Gopinanath, and Mani, K. (), Add-On Security Model for Public-Key Cryptosystem Based on Magic Square Implementation, Proceedings of the World Congress on Engineering and Computer Science 2009 Vol I, WCECS 2009 (October 20-22), San Francisco, USA. Available at (PDF): www.iaeng.org/publication/WCECS2009/WCECS2009_pp317-321.pdf

Huang, Hui-fen (2009), Perceptual Image Watermarking Algorithm Based on Magic Squares Scrambling in DWT, in: INC, IMS and IDC, 2009. NCM '09. Fifth International Joint Conference. Available from IEEE XPlore

Chang, Chin-Chen, et al (2009), An image authentication scheme using magic square, in: 2009 2nd IEEE International Conference on Computer Science and Information Technology. Available from IEEE CS Digital Library

Mathematical definitions from MathWorld: mathworld.wolfram.com/MagicConstant.html
Magic constant formula (looks a bit long?)
see also:
mathworld.wolfram.com/MagicSquare.html
mathworld.wolfram.com/MagicCube.html
Magic Cube def. ("cite this as: Eric W. Weisstein. "Magic Cube." From MathWorld - A Wolfram Web Resource. mathworld.wolfram.com/MagicCube.html)

Pinn, K., Wieczerkowski C., 'Number of Magic Squares From Parallel Tempering Monte Carlo', fr.arxiv.org/abs/cond-mat/9804109/ (abstract)

It has been known since 1693 that there exist 880 basic (excluding those obtained by rotation and reflection ) 4x4 magic squares and 275305224 basic 5x5 magic squares. The number of basic magic squares of any higher degreee is not yet known but it was estimated by Klaus Pinn and C. Wieczerkowski (1998) using Monte Carlo simulation and methods from statistical mechanics to be (1.7745 ± 0.0016) x 10^19 in the 6x6 case squares and (3.7982 ± 0.0004) x 10^34 in the 7x7 case. - Wikipedia magic squares en.wikipedia.org/wiki/Magic_square
see also mathworld.wolfram.com/MagicSquare.html
It is an unsolved problem to determine the number of magic squares of an arbitrary order, but the number of distinct magic squares (excluding those obtained by rotation and reflection) of order n= 1, 2, ... are 1, 0, 1, 880, 275305224, ... (Sloane's A006052; Madachy 1979, p. 87). The 880 squares of order four were enumerated by Frenicle de Bessy in the seventeenth century, and are illustrated in Berlekamp et al. (1982, pp. 778-783). The number of 5x5 magic squares was computed by R. Schroeppel in 1973. The number of 6x6 squares is not known, but Pinn and Wieczerkowski (1998) estimated it to be (1.7745±0.0016) x 10^19 using Monte Carlo simulation and methods from statistical mechanics. Methods for enumerating magic squares are discussed by Berlekamp et al. (1982) and on the MathPages website.

'uLearn Today' www.ulearntoday.com/magazine/physics_article1.jsp?FILE=magicsquares
Good history, some facts not elsewhere, including Cornelius Agrippa (1486-1535) mentioned as the first detailed investigation, and mention of Agrippa constructing squares 'from orders 3 to 9' and Pythagoras, but mostly unreferenced. Also has dates of the first known squares of various orders, although according to an unsupported claim in "project-CSE40476_shirley.pdf" Pythagoras 'allocated the planets to various magic squares' long before (although the first order 5 was not discovered until much later[CHECK DATE].

In 1593, the Chinese mathematician Cheng Ta-wei constructed a 6 by 6 magic square, where every row, column and the main diagonals add up to 111.

There are many varieties of magic squares, which are studied in mathematics. Some simply satisfy the row, column and diagonal sum rules, and are called simple. Others also possess a great deal of symmetry and are called Nasik magic squares [DEFINITION].
The magic square problem is applied in several areas of mathematics such as theories of groups, lattices, Latin squares, determinants, partitions, matrices and congruence arithmetic. Computer scientists are also perplexed by the difficulty of generating all magic squares of larger sizes." - www.math.wichita.edu/~richardson/mathematics/magic%20squares/4th-ordermagicsquares.html
Another observation one can make from these magic squares is the pattern one can get if one traces the position of the numbers 1 through 16 from cell to cell. This was first suggested by Claude Fayette Bragdon, a prominent U.S. architect who lived from 1866 to 1946. Below are the four 4x4 magic squares given above with the paths traced by colored lines. Notice the symmetries that appear. - intro page:
www.math.wichita.edu/~richardson/mathematics/magic%20squares/magicsquares-intro.html William H. Richardson, Associate Professor, Associate Chair and Undergraduate Coordinator, Department of Mathematics and Statistics, Wichita State University (william.richardson@w[...].e[...]).

References to read/check:

Magic circle member Mark Farrar's pages have a history mentioning (but not offering links to) historical sources concerning magic squares, some of which are not found elsewhere.
www.markfarrar.co.uk/msqhst01.htm

There is a good summary and links at: www.ezresult.com/article/Magic_squares

Gnomon Magic Square, MathWorld (1999): A 4 x 4 magic square in which the elements in each 2 x 2 corner have the same sum. Dürer's magic square... is an example of a gnomon magic square since the sums in any of the four quadrants (as well as the sum of the middle four numbers) are all 34 (Hunter and Madachy 1975, p. 24).
Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, 1975. (www.amazon.com/exec/obidos/ASIN/0486231100/weisstein-20)
Eric W. Weisstein. "Dürer's Magic Square." From MathWorld; A Wolfram Web Resource. mathworld.wolfram.com/DuerersMagicSquare.html

A cultural history of Magic squares

Magic matrices, with their almost impenetrable permutations, have a particularly symbol-laden history. The earliest magic square - the order three or Lo Shu is enshrined in China as an integral component of many extant cultural practices such as Feng-Shui (Hean-Tatt 1991), united by the same regard for mathematical precision and inquiry that inspired Leibniz in his development of the binary system that became a crucial component in the development of computing.

[IMG: LoShu]

In the ninth century, Arabian astrologers used magic squares to interpret horoscopes and it is thought that magic squares of order 4 were known before the oldest datable example, documented by Indian polymath Varahamihira around 587 CE. In the doorway to the 8th-century Jain temple at Khajuraho in Madhyar Pradesh there is the first known 'most-perfect' order 4 magic square dated around 1000-1100 CE (photo in header by kind permission of Rainer Typke and Agatha C. Walczak-Typke).

The Indian 'vedic square' (the multiplication table from 1x1 to 9x9 as a matrix of integers reduced to single (digital root) numbers by addition later became a cornerstone of Islamic art (Critchlow 1976) where the central cell of particular order five magic squares - occupied by the number 1 - is left blank as the number of deity.

[IMG: vedic square]

A manuscript, dated 1356, from the Slavonic Gospels contain information about the masnuscript's history, encrypted in a magic square matrix (Elliott).

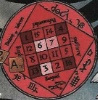
In the 15th century, Cornelius Agrippa (1486-1535) associated the known planets of his time with squares of orders 3-9. The magic square had already been appropriated in some cultures as everyday magical talismans, however:

Three Books of Occult Philosophy is an encyclopedic work drawing on many sources. I would note that the attribution of magic squares to planets is not unique to Agrippa, for example the Liber Angelis, a 15th century manuscript of magic, translated in Claire Fanger's Conjuring Spirits (Penn State 1998) at 65-69 contains almost identical magic squares attributed to the same planets as Three Books of Occult Philosophy. - Christopher Warnock (by email)

The varied glyphs formed by tracing the magic line (where each number from 1-n2 is joined in numerical sequence) have been the subject of complex ritual practices.

[IMG: talisman]

These rich threads of association first surfaced in western art sometime in 1514 behind the famous brooding angel's head in Albrecht Dürer's 'Melancholia'. Setting aside interpretation of the engraving's details, the scene itself is - significantly - said by Frances Yates (reinstating a neglected Renaissance view of melancholy as a portal to wisdom) to depict 'the melancholic inspiration of the artist-scientist' (Yates 1983).

Having appeared in various cultures across the globe, in more recent times one pillar of Gaudi's cathedral in Barcelona displays an (irregular) order four magic square, devised by the sculptor Subirachs.

Later in the 20th century, magic squares and cubes fell out of favour as a serious mathematical topic, until the 1990s when - with increasing computer power and, probably, shifts in current attention - there has been a gradual rekindling of interest and several new findings have emerged. One example (Ollerenshaw and Brée 1998] concerns 'most-perfect' squares of order 4 and above (their proposed terminology). However, knowledge concerning the historically more recent magic cubes and hyper-cubes still lags behind what is known about magic squares (Singmaster 1996), while human inventiveness continues to throw up a dizzying array of other 'magic' figures (Pickover 2001).

References: cultural history

Elliott, Rich, Cryptography, Ciphers, and Hidden Texts, Available at: www.skypoint.com/members/waltzmn/Cryptography.html

Critchlow, Keith. (1976). Islamic Patterns: an Analytical and Cosmological Approach. Inner Traditions, Rochester, Vermont, 1999 (US Reprint).

Hean-Tatt, Ong (1991). The Chinese Pakua: an Exposé. Pelanduk Publications, Selangor Darul Ehsan, Malaysia.

Ollerenshaw, Brée (1998). Most-perfect pandiagonal magic squares. The Institute of Mathematics and its Applications.

Singmaster, David (1996). Queries on sources in recreational mathematics. Section 7.N.1., Earliest magic cubes:

Magic Cubes. Fermat seems to be the first to construct one. However, it fails along 8 of the 24 2-agonals as well as along all 4 3-agonals. Benson & Jacoby cite G. Frankenstein, in the Commercial Traveller (Cincinnati) (11 Mar 1875), for a perfect 83 (NYS). Maxey Brooke cites Joseph Sauvier (1710) for the first magic cube (NYS) and Schlegel (1892) for the first magic 34 (NYS). In W. S. Andrews' Magic Squares and Cubes, C. Planck cites a book of his, Theory of Path Nasiks, NYS, which seems to be the first approach to a theory. Gardner, SA (Feb 1976) says there is an unpublished MS of Rosser & Walker at Cornell and that there are reports by Schroeppel and Beeler on this. Can anyone help find these?

Available at: anduin.eldar.org/~problemi/singmast/queries.html

Pickover, Clifford A. (2001). The Zen of Magic Squares, Circles, and Stars. Princeton University Press.

Yates, Frances A. (1979). The Occult Philosophy in the Elizabethan Age. Ark Paperbacks, London, 1983.

Leibniz and the binary number system

Use material already collected

References: Leibniz and binary

Clarke, J. J., Oriental Enlightenment - the Encounter Between Asian and Western Thought (Routledge, 1997) On Amazon

Feng-Shui and other specific examples

To follow

References Feng-Shui etc.

Wikipedia magic squares en.wikipedia.org/wiki/Magic_square
The Lo-Shu turtle, and use of the 9-fold square in various practices.

Arabic squares, Vedic astrology

Use in Arabian astrology: research if derived from 9-fold square of the Vedic horoscope

[IMG: vedic chart, Arabic chart, 'transitional'(?) 9/13-fold circular chart]

How and when did the (Greek) circular chart take precedence?

Singmaster:
'ARABIC LATIN SQUARES. Ahrens discusses and cites early examples from medieval Islamic times, c1200, when they were used on amulets. Are there other sources, discussions, examples, etc.?'

'Li Yan & Du Shiran's Chinese Mathematics - A Concise History, section 5.6 (and other books) describes 6 x 6 magic squares on iron tablets, using Arabic numerals, found at Xian in 1956. [...] These are apparently in the new museum in Xian.'
- anduin.eldar.org/~problemi/singmast/chinarec.html

5.I. Latin and Euler Squares. Euler's "Recherches sur une nouvelle espece de Quarres Magiques" (1782) appears to be the modern source. But there are pairs of orthogonal 4 by 4 squares in Ozanam (1725) and Alberti (1747). (The pair in Bachet is due to the 1874 editor.) Ahrens says Latin square amulets go back to medieval Islam (c1200) and a magic square of al-Buni, c1200, indicates knowledge of two orthogonal 4 x 4 Latin squares. I have recently found a 7 x 7 Latin square in a Venetian book of 1541 and references to a 4 x 4 Latin square epitaph from Cornwall, 1708, but the references are different - to Meneage parish church, St. Mawgan and to Cunwallow, near Helstone. Can anyone provide clear information on this? Are there any other early western usages of Latin squares?
- anduin.eldar.org/~problemi/singmast/queries.html

References: Arabic squares/Astrology

Wilde, George (1901). p38. Chaldean Astrology up to Date. E. Marsh-Stiles, London and the Occult Book Co., Halifax.]

Wikipedia, magic squares. The use of the 9-fold square in various practices including Arabian astrology. Available at en.wikipedia.org/wiki/Magic_square

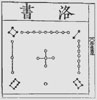
The Khajuraho magic square

This is the earliest known example of a most-perfect order 4 square (most-perfect squares have extra mathematical properties). Khajuraho square:

7	12	1	14
2	13	8	11
16	3	10	5
9	6	15	4

[IMG: Khajuraho square in Jain temple]

References: Khajuraho square

The Khajuraho square is also a so-called diabolic or panmagic (pandiagonal magic square) where, in addition to the rows, columns and main diagonals, the broken diagonals also have the same sum.
- Wikipedia, magic squares en.wikipedia.org/wiki/Magic_square

Cornelius Agrippa

(1486-1535) Associated the 7 magic squares of orders 3-9 to Saturn, Jupiter, Mars, Sun, Venus, Mercury, and the Moon., but drew on earlier works, possibly including the Liber Angelis.

References: Agrippa

To follow

Magical talismans

To follow

References: Magical talismans

To follow

Subirachs' magic square

See details.

References: Subirachs' square

The magic sum of the square is 33, the age of Jesus at the time of the Passion. Structurally, it is very similar to the Melancholia magic square, [except reversed laterally and vertically] but it has had the numbers in four of the cells reduced by 1 [to make 33 the magic constant, but not a true magic square as the numbers are not sequential].

- Wikipedia magic squares en.wikipedia.org/wiki/Magic_square
Also see the site with animations of this square.

Melancholia

The delicately-balanced state of melancholy can become something impenetrable and dense when denied a creative outlet, and the work and temperament of that previous wave of artist-researchers (with Dürer and his engraving acting as a portal), with Burton's historical tome on the subject (Burton 1621) have become standard references to the state, as well as Cranach's 4 paintings on the subject of around 1530: The Melancholy Witch

References: Melancholia

Burton, Robert (1621), The Anatomy of Melancholy. New York Review Books, New York, 2001

Durer's engravings. Web Museum, Paris. www.ibiblio.org/wm/paint/auth/durer/engravings/

Wikipedia, magic squares. Dürer's square mathematics:

The sum 34 can be found in the rows, columns, diagonals, any 2x2 block of numbers, the sum of the four corners, the sums of the four outer numbers clockwise from the corners (3 + 8 + 14 + 9) and likewise the four counter-clockwise, and the sum of the middle two entries of the two outer columns and rows (eg 5 + 9 + 8 + 12), as well as several kite-shaped quartets, eg 3 + 5 + 11 + 15

Available at en.wikipedia.org/wiki/Magic_square

Wikipedia, magic squares. Page on Durer, melancholy and a debated new Picasso painting: 'Melencolia' (SIC) (www.web.org.uk/picasso/melencolia.html)
on 'The Picasso Conspiracy' website web.org.uk/picasso/Welcome.html

Dürer's theme of Saturnalian Melancholy appears to have been derived from a treatise by a German physician named Heinrich von Nettesham, written around 1510, and entitled 'De occulta philosophia.'

Since classical times artistic Melencolia was thought of as a depressed state of mind that takes away an artist's enthusiasm for his work. It's cure was believed by Renaissance astrologer's to be aided by the charm of a magic square and in particular the Jupiter magic square which appears in the upper right hand corner of Durer's engraving.

David Singmaster has one of the world's best collections of recreational mathematics and puzzle books.

'According to Singmaster, one of the first European manuscripts to deal with magic squares is a fifteenth-century Latin manuscript in Cracow (which incidentally gives the famous 4 x 4 square that occurs in Dürer's print Melancholia)' [1514, so he may have seen the latter, although he is also known to have been influenced by Agrippa and possibly his sources]

- SINGMASTER, D. (1993), Sources in Recreational Mathematics: An Annotated Bibliography, Sixth Preliminary Edition, School of Computing, Information Systems and Mathematics, South Bank University, London, (SE1 0AA), 1993.
- from Pickover, Clifford (2001). The Zen of Magic Squares, Circles, and Stars. Princeton University Press. Reviewed by Andrew Bremner (downloaded as rev-bremner.pdf) from www.ams.org/notices/200303/rev-bremner.pdf