Line and row transposition in magic square pattern transformation
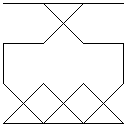
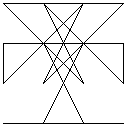
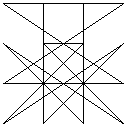
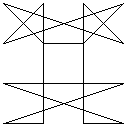
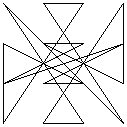
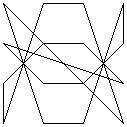

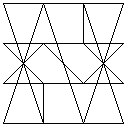
The magic line images above were formed by successive transpositions of rows and columns (in the established manner). Note that these transpositions preserve the bilateral and reflectional symmetry of the given square. The suggestion is that the symmetry pattern of the magic line (or - yet to be tested - lack of it in magic squares with assymetrical magic line patterns) is a fundamental, not a trivial, property of any given magic square; this assertion would be disproved if such translations were to create an asymmetrical pattern from a symmetrical original square, or vice-versa.
TODO: generate a similar image series for a 4 x 4 square with an asymmetrical magic line pattern)
A further finding (not shown here) based on the magic line suggests that it is possible to group related squares (specifically, to date: order 5 pan-magic squares as a test set) so that the variations are reduced to 20% of the original number. Current work is determining the results of extending this transposition to doubly- and singly-even orders. More information and diagrams will follow further (methodical but long-winded) research, once complete.
Images were generated by a magic square HyperCard stack (Apple classic only - currently being rewritten as a cross-platform and/or web-based application).
